微磁学是研究磁性材料微观磁化行为的重要领域，数值模拟是微磁学研究的主要工具。传统微磁学模拟基于朗道-利夫希兹-吉尔伯特（LLG）方程，计算复杂度高，无法处理大尺度样本，极大影响了微磁学的实用价值。近日，昆明理工大学和清华大学联合团队在《自然·机器智能》杂志发表封面文章，将微磁学模拟的计算复杂度从O(n log(n))降低到了O(N)，为研究大尺度复杂磁性系统打开了大门。文章第一作者为昆明理工大学的蔡云麒副教授（原清华大学博士后，现为中科院物理所副研究员），昆明理工大学材料与工程学院的李江南副教授和清华大学信息国家研究中心王东副研究员为共同通讯作者。

传统微磁学模拟

在磁性材料中，磁畴和磁滞等微观现象决定了材料的宏观磁性特征。微磁学通过计算机模拟对这些微观行为进行推演，从而帮助科学家和工程师设计更高效的磁存储设备、磁传感器和其他磁性器件。

微磁学模拟的理论基础是朗道-利夫希茨-吉尔伯特（LLG）方程：

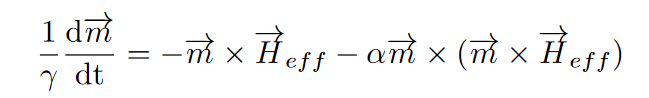
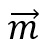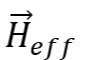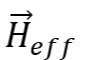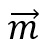       方程中的为磁化向量，为等效场。注意，本身也是的函数，因此，LLG方程刻画了磁介质与磁场相互作用的基本物理规律，可以描述磁场演化的动态过程。

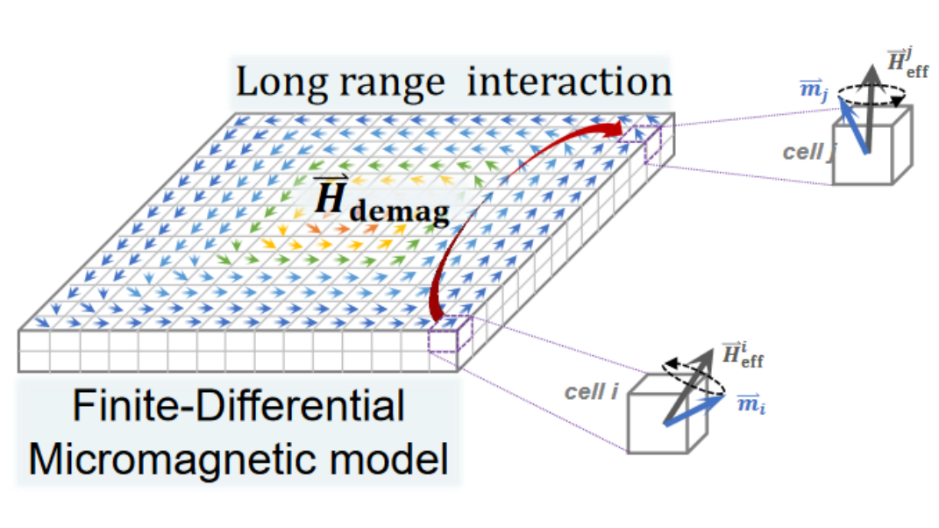
       LLG方程中的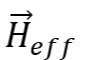包含外磁场、各向异性场、交换场和静磁场，其中静磁场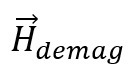要考虑磁介质中任意两个位置的相互作用。如果我们将磁介质分成N个微小单元的话，每个单元的静磁场计算公式如下：

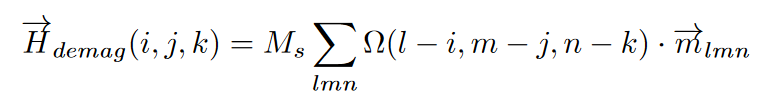
       其中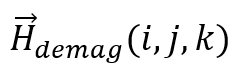为在位置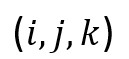处的静磁场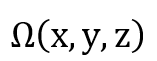，描述了距离向量为[x,y,z]的两个单元之间的静磁作用矩阵。显然，要想完成一次静磁场计算，需要计算N2次单元相互作用，即这一计算的复杂度为O(N2)。特别是，单元之间的作用强度随距离r以反比率（1/r）衰减，这意味着遥远处的静磁作用也会累积成显著影响，不能简单忽略。

       为了加快静磁场计算，研究者提出了快速傅里叶变换（FFT）方法。这一方法的基本思路是将静磁场计算视为当前磁化向量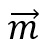与单元间相互作用矩阵Ω的卷积，这一卷积可以通过FFT转换成乘法计算，从而将计算量降到O(n log(n))。尽管如此，这一计算复杂度对于大尺度磁样本依然是不可接受的。

深度学习方法

       本文提出一种层次性计算方案，将磁化向量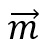通过下采样方式逐层降低解析度，解析度越低，每个格子覆盖的视野越大。每一层计算只考虑近邻相互作用，再将不同层的相互作用累加起来。简单地说，这种方案把静磁场的计算拆分成不同尺度下局部静磁相互作用的累加，用这种累加来近似复杂的全局卷积计算。

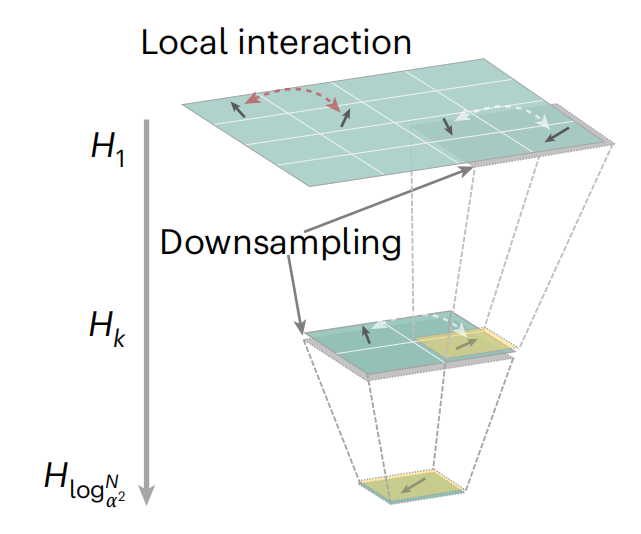
文章提出了一种U型神经网络（Unet）来实现上述计算方案。理论分析表明，在合理的设计下，这一方法可以将计算复杂度降低到O(N)，从而使大尺度样本的微磁学模拟成为可能。

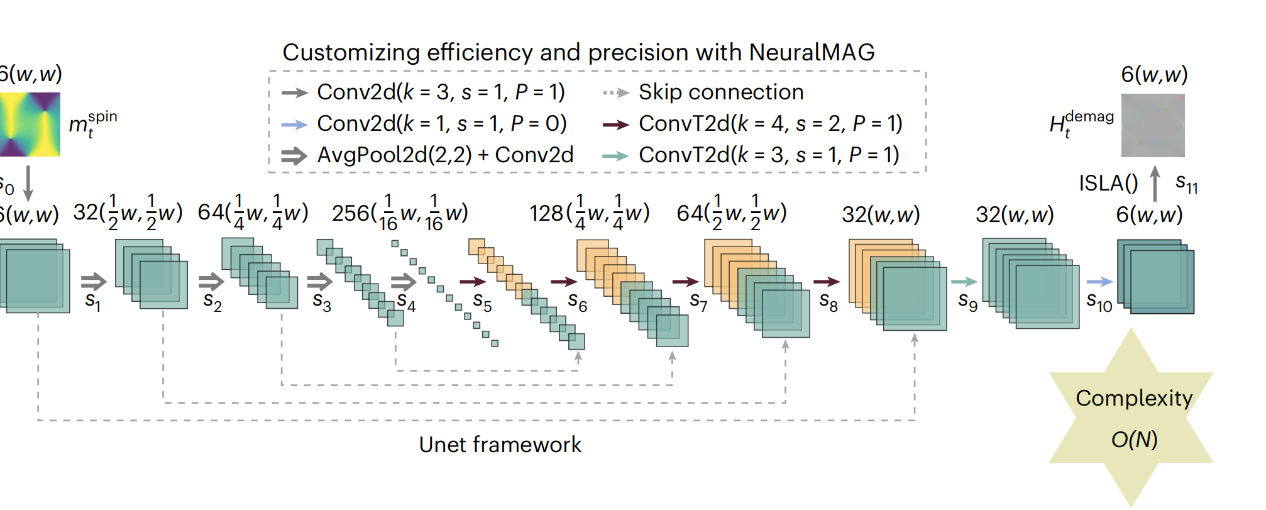
上图是Unet结构示意图，包括编码器和解码器两部分：

编码器：提取不同尺度下的磁化信息，学习不同尺度下的局部相互作用规则并保存在卷积核中。

解码器：将这些局部相互作用在各个尺度上进行累积，用反卷积来实现累加时的局部调整。

和其他针对特定任务的神经网络方法不同，本文提出的方法依然保持LLG方程的基础框架，神经网络只专注于核心计算部分，即静磁场的计算。这使得它具有很强的通用性，同一个模型可以用于不同尺寸、不同形状和不同材料参数的微磁学模拟。该计算框架称为NeuralMag，代码已经开源。

实验验证

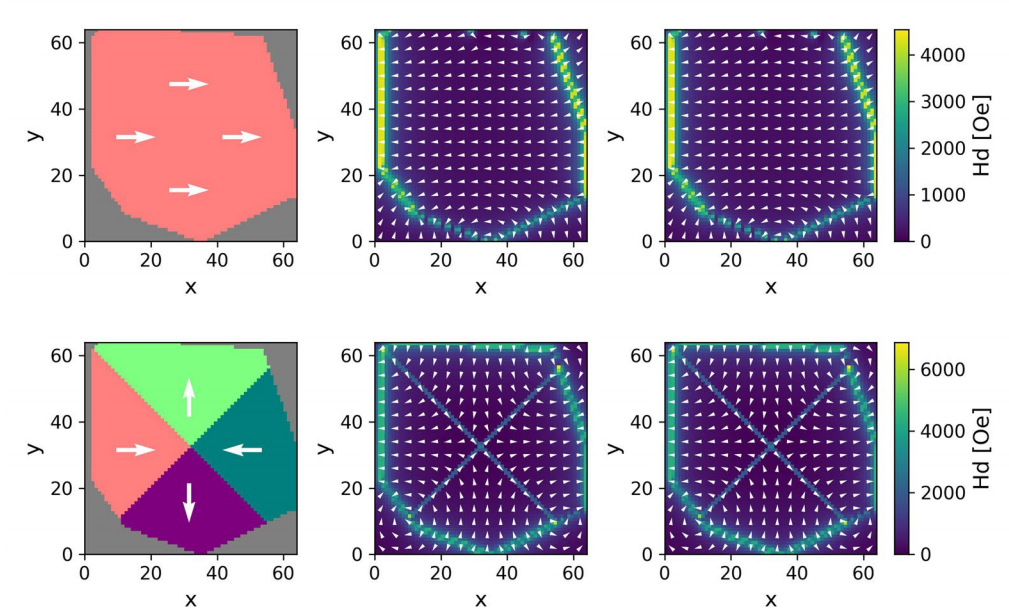
文章通过训练一个单一的Unet模型，测试了NeuralMag在不同任务和条件下的表现。结果显示，NeuralMag在精度上也与传统方法接近，且计算速度显著提升。例如，下图是一个随机形状的样本基于传统FFT方法（上一列）和基于NeuralMag方案在迭代同样次数后的磁化向量。可以看到，NeuralMag的结果与传统方法极为相似，但静磁场的计算速度可提升5倍以上，内存占用也更少。特别是，当样本的大小到3072之后，传统FFT方法因内存和速度原因已经无法计算，但NeuralMag依然可以在合理时间内完成计算。

展望

NeuralMag的出现，为微磁学模拟打开了新局面。通过结合深度学习和物理学的基本原理，它为解决长期存在的计算瓶颈提供了创新的解决方案。更重要的是，长程相互作用的计算复杂性在物理、化学的很多领域都是亟待解决的问题，本文提出的用神经网络分层累加以近似长程相互作用的方案具有普遍价值。

论文地址：https://www.nature.com/articles/s42256-024-00914-7

Arxiv版本: https://arxiv.org/pdf/2410.14986

代码开源地址：https://github.com/Caiyq2019/NeuralMAG/tree/main/

供稿 | 具身智能技术交叉创新群体
编辑 | 李琳
审核 | 丁贵广